Skip to main content
SpringerLink
Log in

Application of radial basis functions and sinc method for solving the forced vibration of fractional viscoelastic beam

  • Published:
Journal of Mechanical Science and Technology Aims and scope Submit manuscript

Abstract

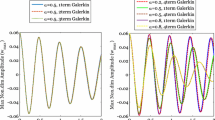
In this paper, the forced vibrations of the fractional viscoelastic beam with the Kelvin-Voigt fractional order constitutive relationship is studied. The equation of motion is derived from Newton’s second law and the Galerkin method is used to discretize the equation of motion in to a set of linear ordinary differential equations. For solving the discretized equations, the radial basis functions and Sinc quadrature rule are used. In order to show the effectiveness and accuracy of this method, some test problem are considered, and it is shown that the obtained results are in very good agreement with exact solution. In the following, the proposed numerical solution is applied to exploring the effects of fractional parameters on the response of the beam and finally some conclusions are outlined.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Y. A. Rossikhin and M. V. Shitikova, Applications of fractional calculus to dynamic problems of linear and nonlinear hereditary mechanics of solids, Applied Mechanics Reviews, 50 (1) (1997) 15–67.

    Article  MathSciNet  Google Scholar 

  2. Y. A. Rossikhin and M. V. Shitikova, Application of fractional calculus for dynamic problems of solid mechanics: novel trends and recent results, Applied Mechanics Reviews, 63 (1) (2010) 010801.

    Article  Google Scholar 

  3. Z. Zheng-You, L. Gen-Guo and C. Chang-Jun, Quasi-static and dynamical analysis for viscoelastic Timoshenko beam with fractional derivative constitutive relation, Applied Mathematics and Mechanics, 23 (1) (2002) 1–12.

    Article  Google Scholar 

  4. G. G. Li, Z. Y. Zhu and C. J. Cheng, Application of Galerkin method to dynamical behavior of viscoelastic Timoshenko beam with finite deformation, Mechanics of Time-Dependent Materials, 7 (2) (2003) 175–188.

    Article  Google Scholar 

  5. O. P. Agrawal, Analytical solution for stochastic response of a fractionally damped beam, Journal of Vibration and Acoustics, 126 (4) (2004) 561–566.

    Article  Google Scholar 

  6. A. Galucio, J. Deu and R. Ohayon, A fractional derivative viscoelastic model for hybrid active-passive damping treatments in time domain-application to sandwich beams, Journal of Intelligent Material Systems and Structures, 16 (1) (2005) 33–45.

    Article  Google Scholar 

  7. F. Cortés and M. J. Elejabarrieta, Homogenized finite element for transient dynamic analysis of unconstrained layer damping beams involving fractional derivative models, Computational Mechanics, 40 (2) (2007) 313–324.

    Article  MATH  Google Scholar 

  8. K. S. Hedrih, The transversal creeping vibrations of a fractional derivative order constitutive relation of nonhomogeneous beam, Mathematical Problems in Engineering (2006).

    Google Scholar 

  9. Z. F. Liang and X. Y. Tang, Analytical solution of fractionally damped beam by Adomian decomposition method, Applied Mathematics and Mechanics, 28 (1) (2007) 219–228.

    Article  MathSciNet  MATH  Google Scholar 

  10. F. Cortés and M. J. Elejabarrieta, Structural vibration of flexural beams with thick unconstrained layer damping, Journal of Mechanical Science and Technology, 25 (8) (2011) 1893–1904.

    Article  MATH  Google Scholar 

  11. B. C. Jung, D. Lee, B. D. Youn and S. Lee, A statistical characterization method for damping material properties and its application to structural-acoustic system design, Boundary Value Problems, 2012 (1) (2012) 1–13.

    Article  Google Scholar 

  12. I. Abu-Alshaikh, A. N. Al-Rabadi and H. S. Alkhaldi, Dynamic response of a beam with absorber exposed to a running force: Fractional calculus approach, ASME 2012 International Mechanical Engineering Congress and Exposition (2012).

    Google Scholar 

  13. T. Z. Yang and B. Fang, Stability in parametric resonance of an axially moving beam constituted by fractional order material, Archive of Applied Mechanics, 82 (12) (2012) 1763–1770.

    Article  MathSciNet  MATH  Google Scholar 

  14. M. Alvelid, Sixth order differential equation for sandwich beam deflection including transverse shear, Composite Structures, 102 (1) (2013) 29–37.

    Article  Google Scholar 

  15. S. M. S. Bahraini, S. Eghtesad, Farid M. and M. Ghavanloo, Large deflection of viscoelastic beams using fractional derivative model, Journal of Mechanical Science and Technology, 27 (4) (2013) 1063–1070.

    Article  Google Scholar 

  16. D. Behera and S. Chakraverty, Numerical solution of fractionally damped beam by homotopy perturbation method, Central European Journal of Physics, 11 (6) (2013) 792–798.

    Google Scholar 

  17. M. Di Paola, R. Heuer and A. Pirrotta, Fractional viscoelastic Euler–Bernoulli beam, International Journal of Solids and Structures, 50 (22) (2013) 3505–3510.

    Article  Google Scholar 

  18. D. Liu, W. Xu and Y. Xu, Stochastic response of an axially moving viscoelastic beam with fractional order constitutive relation and random excitations, Acta Mechanica Sinica, 29 (3) (2013) 443–451.

    Article  MathSciNet  MATH  Google Scholar 

  19. Y. Wang and D. J. Inmanb, Experimental and Finite Element Analysis for a Multifunctional Beam with Frequencydependent Viscoelastic Behavior (2013).

    Google Scholar 

  20. S. Di Lorenzo, M. Di Paola, F. P. Pinnola and A. Pirrotta, Stochastic response of fractionally damped beams, Probabilistic Engineering Mechanics, 35 (1) (2014) 37–43.

    Article  Google Scholar 

  21. G. E. Fasshauer, Mesh free approximation methods with MATLAB, World Scientific, 6 (2007).

  22. H. Wendland, Scattered data approximation, Cambridge University Press (2004).

    Book  MATH  Google Scholar 

  23. A. Fedoseyev, M. Friedman and E. Kansa, Improved multi quadric method for elliptic partial differential equations via PDE collocation on the boundary, Computers & Mathematics with Applications, 43 (3) (2002) 439–455.

    Article  MathSciNet  MATH  Google Scholar 

  24. J. Yoon, Spectral approximation orders of radial basis function interpolation on the Sobolev space, SIAM Journal on Mathematical Analysis, 33 (4) (2001) 946–958.

    Article  MathSciNet  MATH  Google Scholar 

  25. F. Stenger, Numerical methods based on sinc and analytic functions, Springer Science & Business Media, 20 (2012).

  26. J. Lund and K.L. Bowers, Sinc methods for quadrature and differential equations, SIAM (1992).

    Book  MATH  Google Scholar 

  27. K. i. Tanaka, M. Sugihara, K. Murota and M. Mori, Function classes for double exponential integration formulas, Numerische Mathematik, 111 (4) (2009) 631–655.

    Article  MathSciNet  MATH  Google Scholar 

  28. M. Sugihara and T. Matsuo, Recent developments of the Sinc numerical methods, Journal of Computational and Applied Mathematics, 164 (1) (2004) 673–689.

    Article  MathSciNet  MATH  Google Scholar 

  29. M. Mori and M. Sugihara, The double-exponential transformation in numerical analysis, Journal of Computational and Applied Mathematics, 127 (1) (2001) 287–296.

    Article  MathSciNet  MATH  Google Scholar 

  30. A. Galucio, J. F. Deü, S. Mengué and F. Dubois, An adaptation of the Gear scheme for fractional derivatives, Computer Methods in Applied Mechanics and Engineering, 195 (44) (2006) 6073–6085.

    Article  MathSciNet  MATH  Google Scholar 

  31. S. Di Lorenzo, F. P. Pinnola and A. Pirrotta, On the dynamics of fractional viscoelastic beams, ASME 2012 International Mechanical Engineering Congress and Exposition (2012).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Aerospace Engineering Dept., Sharif University of Tech., Azadi Ave., Tehran, 11155-8639, Iran

    M. R. Permoon & H. Haddadpour

  2. School of Mathematics, Iran University of Science and Technology, Narmak, Tehran, 168613114, Iran

    J. Rashidinia, A. Parsa & R. Salehi

Authors
  1. M. R. Permoon
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. J. Rashidinia
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. A. Parsa
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. H. Haddadpour
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. R. Salehi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to H. Haddadpour.

Additional information

Recommended by Associate Editor Eung-Soo Shin

Hassan Haddadpour received his B.Sc. in Mechanical Engineering in 1993 from Abadan Institute of Technology in Iran. He also graduated from the M.Sc. degree program and Ph.D. for Mechanical Engineering in the applied design course from University of Tehran. He joined Sharif University of Technology in 2002. Currently, he is a professor in the Department of Aerospace Engineering of Sharif University of Technology. His research interests are Aeroelasticity, Reduced Order Modeling and Structural Dynamics.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Permoon, M.R., Rashidinia, J., Parsa, A. et al. Application of radial basis functions and sinc method for solving the forced vibration of fractional viscoelastic beam. J Mech Sci Technol 30, 3001–3008 (2016). https://doi.org/10.1007/s12206-016-0306-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12206-016-0306-3

Keywords

Search

Navigation